GEOMETRY ON THE LANDSCAPE

The West Coast of the United States follows a perfect arc with the Great Divide Basin in Southwestern Wyoming, a geographical landmark, at its geometric center; it even touches the northern end of the Bay of California in Mexico:

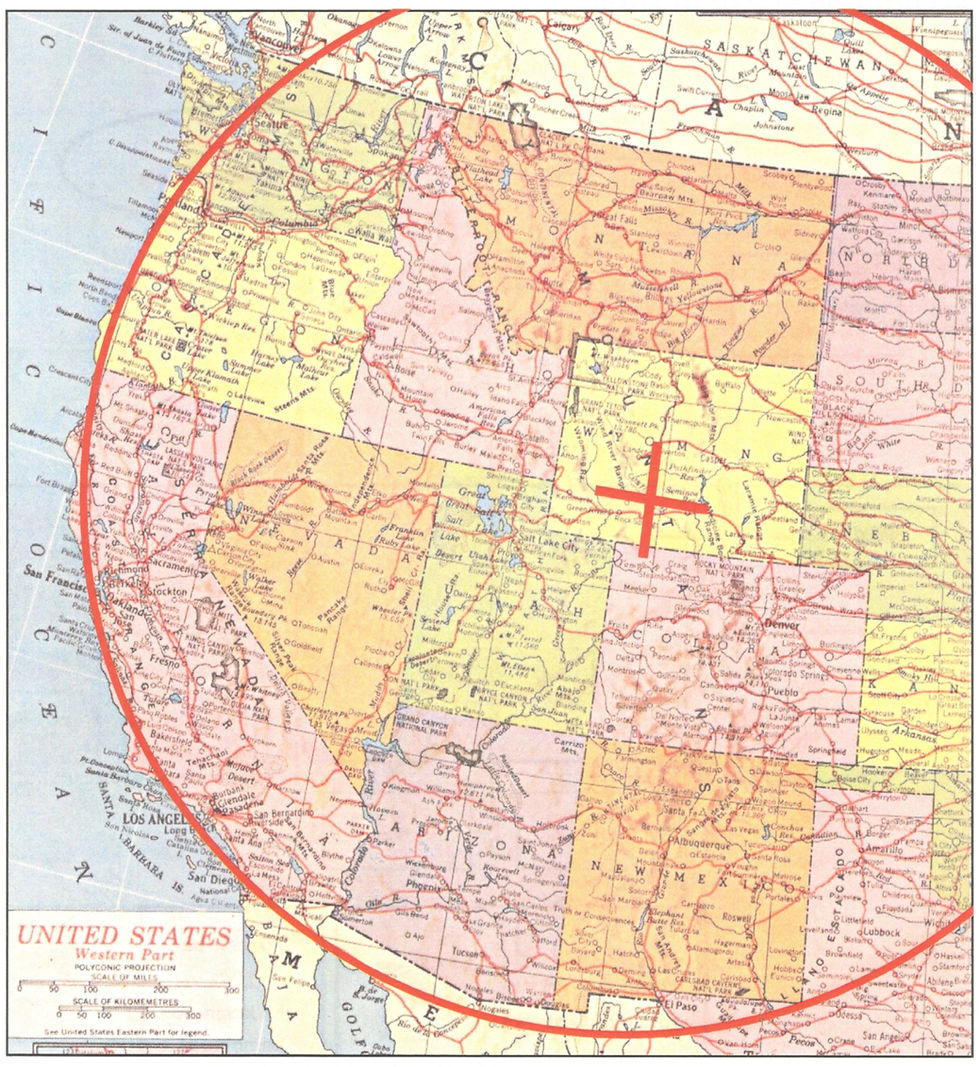
Strangely, the Great Divide Basin is conveniently located by projecting the continuous northern borders of California, Nevada, and Utah into Southwestern Wyoming to get the Basin's latitudinal position, and then projecting the small vertical portion of the southern border of New Mexico into Wyoming to get its longitudinal.

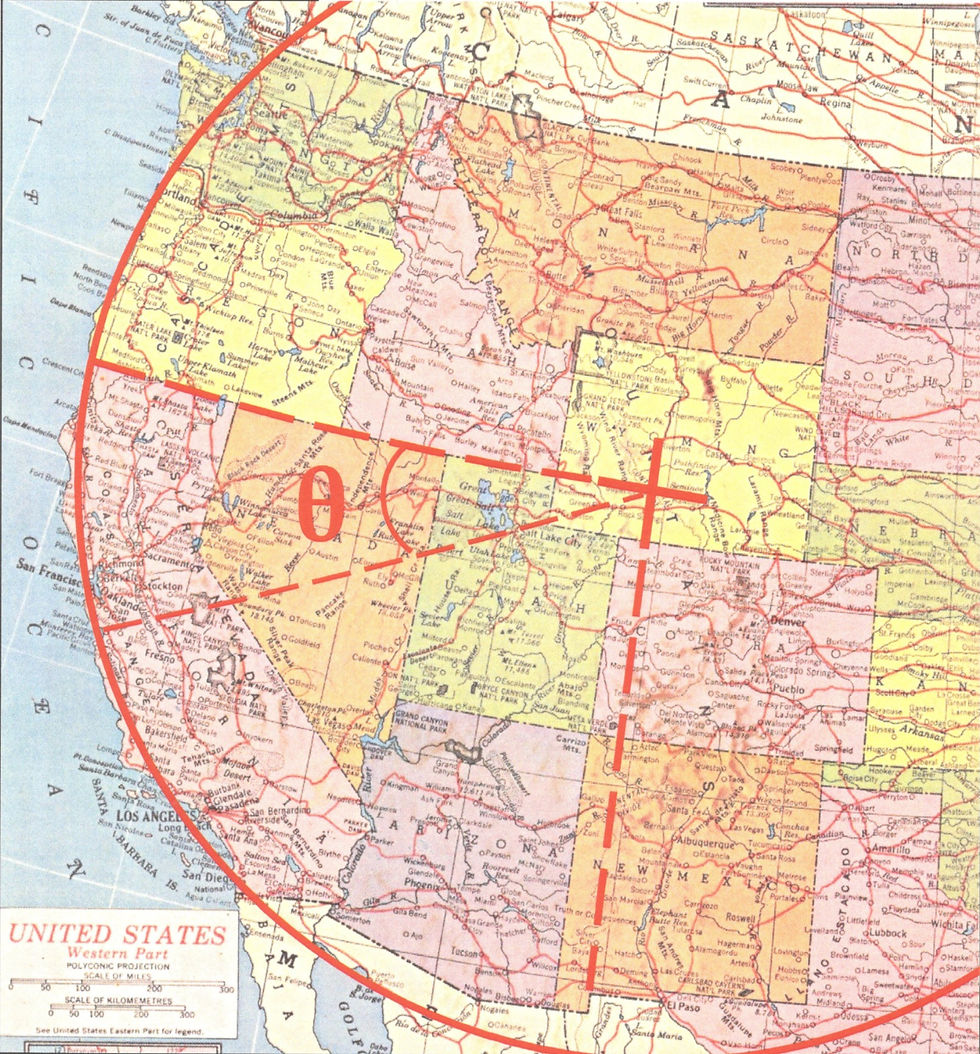
To prove that the arc is real, I have derived two equations for calculating the latitudinal and longitudinal positions of any point on the arc.

Given an angle theta from the horizontal --- the horizontal being defined by the continuous northern borders of California, Nevada, and California --- the LATITUDE of a point on the arc may be calculated using the first of these two equations, and the LONGITUDE by plugging this LATITUDE and the same angle theta into the second:

Using these equations, I have taken the liberty of generating the following table showing the positions of points on the arc, as well as the nearest communities to these points:

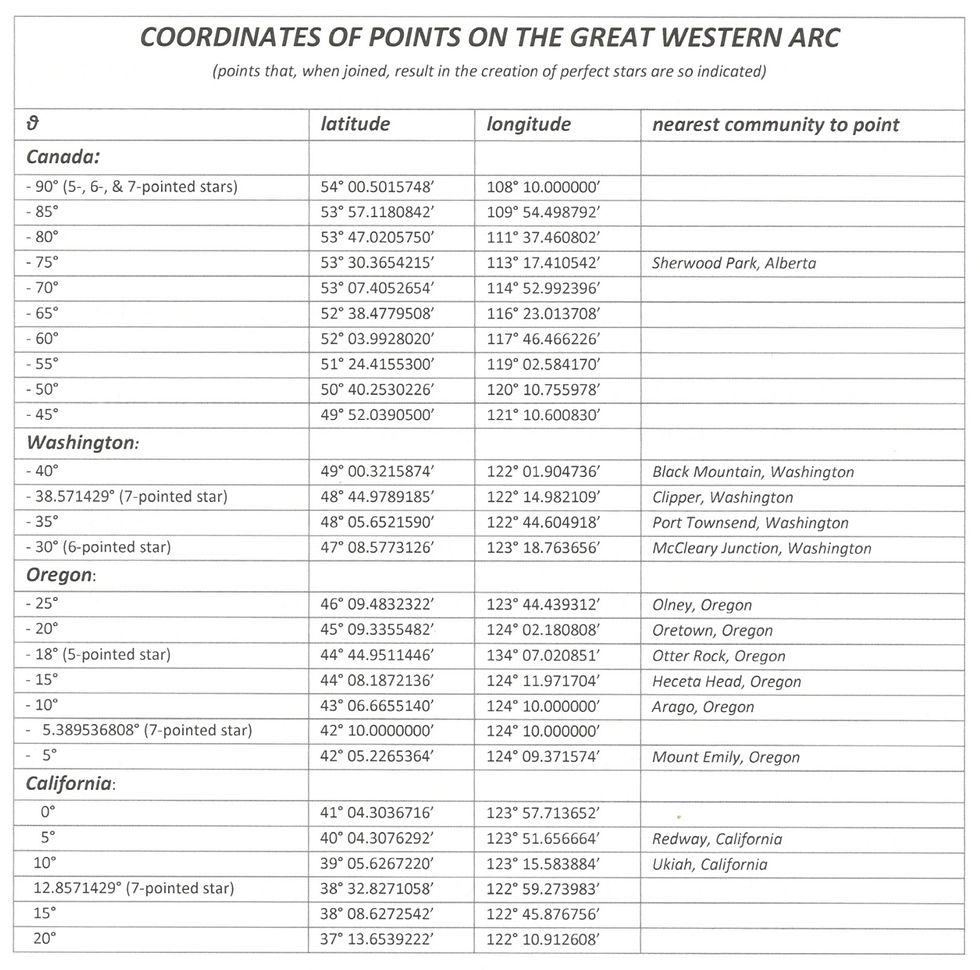
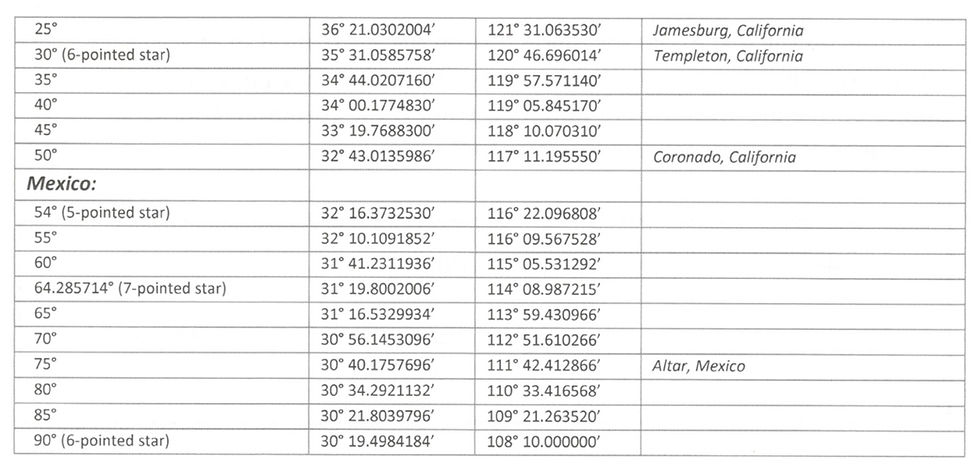
There is no known geological phenomenon to account for the arc, nor any explanation for why the northern borders of California, Nevada, and Utah should have been arranged to point to the Basin's position.

Another example of geometry on the landscape may be found under the blog THE DRAGON (https://www.sealpyramid.com/post/the-dragon).